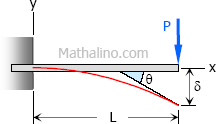

Case 1: Concentrated load at the free end of cantilever beam
Maximum Moment
$M = -PL$
Slope at end
$\theta = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(3L - x)$
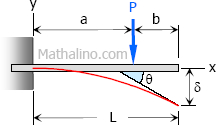
Case 2: Concentrated load at any point on the span of cantilever beam
Maximum Moment
$M = -Pa$
Slope at end
$\theta = \dfrac$
Maximum deflection
$\delta = \dfrac(3L - a)$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(3a - x) \text < for >0 \lt x \lt a$
$EI \, y = \dfrac(3x - a) \text < for >a \lt x \lt L$
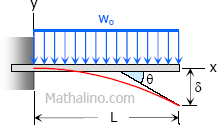
Case 3: Uniformly distributed load over the entire length of cantilever beam
Maximum Moment
$M = -\dfrac$
Slope at end
$\theta = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(6L^2 - 4Lx + x^2)$
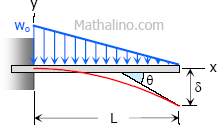
Case 4: Triangular load, full at the fixed end and zero at the free end, of cantilever beam
Maximum Moment
$M = -\dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(10L^3 - 10L^2x + 5Lx^2 - x^3)$
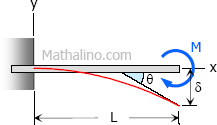
Case 5: Moment load at the free end of cantilever beam
Maximum Moment
$M = -M$
Slope at end
$\theta = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac$

Case 6: Concentrated load at the midspan of simple beam
Maximum Moment
$M = \dfrac$
Slope at end
$\theta_L = \theta_R = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(\fracL^2 - x^2) \text < for >0 \lt x \lt \fracL$
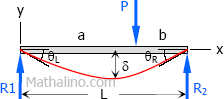
Case 7: Concentrated load at any point on simple beam
Maximum Moment
$M = \dfrac \text < at >x = a$
Deflection at the center (not maximum)
$\delta = \dfrac(3L^2 - 4b^2) \text < when >a \gt b$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(L^2 - x^2 - b^2) \text < for >0 \lt x \lt a$
$EI \, y = \dfrac \left[ \dfrac(x - a)^3 + (L^2 - b^2)x - x^3 \right] \text < for >a \lt x \lt L$
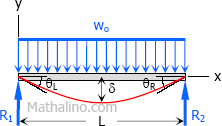
Case 8: Uniformly distributed load over the entire span of simple beam
Maximum Moment
$M = \dfrac$
Slope at end
$\theta_L = \theta_R = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(L^3 - 2Lx^2 + x^3)$
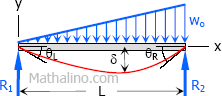
Case 9: Triangle load with zero at one support and full at the other support of simple beam
Maximum Moment
$M = \dfrac>$
Maximum deflection
$\delta = \dfrac \text < at >x = 0.519L$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(7L^4 - 10L^2x^2 + 3x^4)$
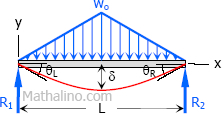
Case 10: Triangular load with zero at each support and full at the midspan of simple beam
Maximum Moment
$M = \dfrac$
Slope at end
$\theta_L = \theta_R = \dfrac$
Maximum deflection
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(25L^4 - 40L^2x^2 + 16x^4) \text < for >0 \lt x \lt \dfrac$
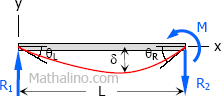
Case 11: Moment load at the right support of simple beam
Maximum Moment
$M = M$
Slope at end
$\theta_L = \dfrac$
Maximum deflection
$\delta = \dfrac \, EI> \text < at >x = \dfrac>$
Deflection at the center (not maximum)
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac\left( 1 - \dfrac \right)$
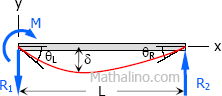
Case 12: Moment load at the left support of simple beam
Maximum Moment
$M = M$
Slope at end
$\theta_L = \dfrac$
Maximum deflection
$\delta = \dfrac \, EI> \text < at >x = \left( L - \dfrac> \right)$
Deflection at the center (not maximum)
$\delta = \dfrac$
Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac(L - x)(2L - x)$